SSD

除了 YOLO 系列，Single Shot MultiBox Detector(SSD) 也算是 one-stage 目标检测算法的先行者了，相比于 YOLO v1 和 Faster R-CNN，其主要特点是：

1. 在 one-stage 算法中引入了多尺度预测(主要是为了克服 CNN 不具有尺度不变性问题)

2. 参考 FasterRCNN 中 anchor 的概念，将其引入 one-stage 中，通过在每个特征图位置设置不同个数、不同大小和不同比例的 anchor box 来实现快速收敛和优异性能

3. 采用了大量有效的数据增强操作

4. 从当时角度来看，速度和性能都超越当时流行的 YOLOV1 和 FasterRCNN

即使到目前为止，多尺度预测加上 anchor 辅助思想依然是主流做法。

1 算法分析

当时主流算法输出形式如下：

而 SSD 的多尺度预测简要流程如下：

相比于 YOLOV1，其差别如下：

主要差别在于 (1)多尺度预测; (2)引入了 anchor；(3) 全卷积形式，接下来按照目标检测通用算法流程思路来讲解。ssd 也是包括 backbone、head、正负样本定义、bbox 编解码和 loss 设计 5 个部分。

1.1 backbone 设计

SSD 的骨架是 VGG16，其是当前主流的分类网络，其主要特点是全部采用 3x3 的卷积核，然后通过多个卷积层和最大池化层堆叠而成，是典型的直筒结构。VGG16 是在 ILSVRC CLS-LOC 数据集上预训练过，为了更加适合目标检测，作者进行了适当扩展：

(1) 借鉴 DeepLab-LargeFOV 思想，将 VGG16 的全连接层 fc6 和 fc7 转换成 3x3 卷积层 conv6 和 1x1 的 conv7，同时将池化层 pool5 由原来的 stride=2 的 2x2 变成 stride=1 的 3x3，为了配合这种变化，对 conv6(3x3 卷积且空洞率为 6)采用了空洞卷积，其在不增加参数与模型复杂度的条件下指数级扩大卷积的视野，其使用扩张率(dilation rate)参数来表示扩张的大小。

(2) 然后移除原始 vgg 的 dropout 层和 fc8 层，并新增一系列卷积层，在检测数据集上做微调。SSD 算法包括两个模型分别是 SSD300 和 SSD512，后面数字表示输入图片 size，这两个模型都是新增一系列卷积层，但是 SSD512 模型新增的卷积会多一些，其余都是完全相同。

(3) 新增的一系列卷积层中除了卷积层外不含有其他部件，如果需要下采样是通过 3x3 且 stride=2 的卷积实现，具体配置如下：

extra_setting = {
    300: (256, 'S', 512, 128, 'S', 256, 128, 256, 128, 256),
    512: (256, 'S', 512, 128, 'S', 256, 128, 'S', 256, 128, 'S', 256, 128),
}

S 表示需要进行下采样。具体细节请看上图的详细结构图，里面有绘制卷积参数。VGG16 在当时是主流网络，但是由于其参数量巨大且网络比较浅，特征提取和感受野比较有限，现在主流骨架网络基本都是 resnet 及其改进版本。

假设是SSD300，那么一共包括 6 个输出特征图，分别命名为 conv4_3、conv7、conv8_2、conv9_2、conv10_2 和 conv11_2，其 wh 大小分别是 38x38、19x19、10x10、5x5、3x3 和 1x1，而SSD512 包括 7 个输出特征图，命名论文中没有给出，其 wh 大小分别是 64x64、32x32、16x16、8x8、4x4、2x2、1x1。

需要注意的是：作者实验发现，conv4_3 层特征图比较靠前，其 L2 范数值(平方然后开根号)相比其余输出特征图层比较大，也就是数值不平衡，为了更好收敛，作者对 conv4_3+relu 后的输出特征图进行 l2 norm 到设置的初始 20 范围内操作，并且将 20 这个数作为初始值，然后设置为可学习参数。

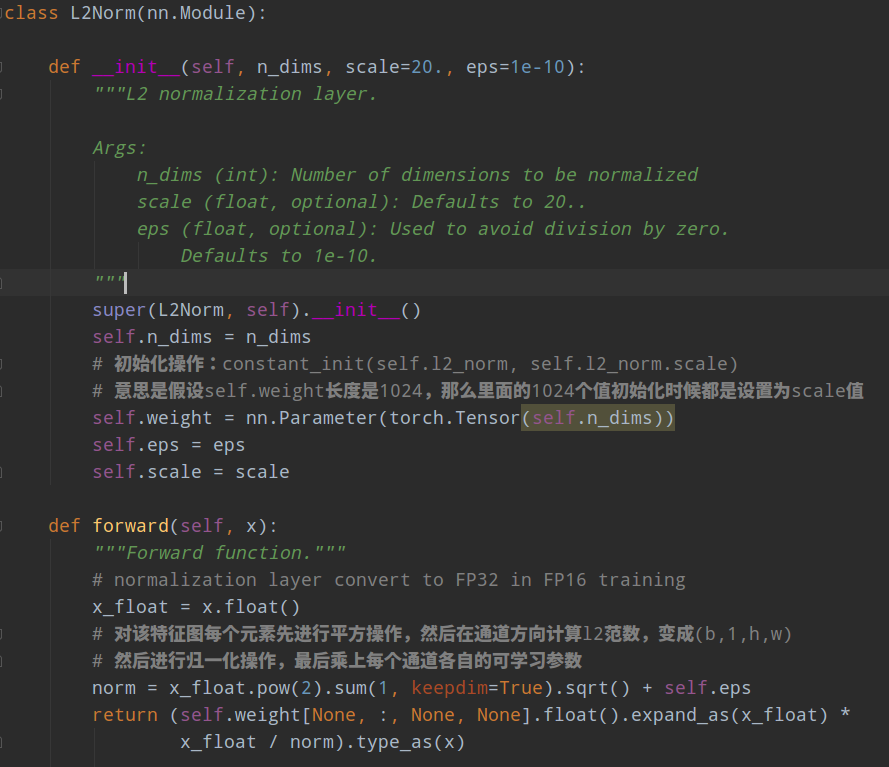
1.2 head 设计

backbone 模块会输出 n 个不同尺度的特征图，head 模块对每个特征图进行处理，输出两条分支：分类和回归分支。假设某一层的 anchor 个数是 m，那么其分类分支输出 shape=(b,(num_cls+1)*m,h',w')，回归分支输出 shape=(b,4*m,h',w')。

1.3 正负样本定义

在说明正负样本定义前，由于 SSD 也是基于 anchor 变换回归的，而且其有一套自己根据经验设定的 anchor 生成规则，故需要先说明 anchor 生成过程。anchor 的可视化如下：

就是对输出特征图上面任何一点，都铺设指定数目，但是不同大小、比例的先验框 anchor。

对于任何一个尺度的预测分支，理论上 anchor 设置的越多，召回率越高，但是速度越慢。为了速度和精度的平衡，作者在不同层设置了不同大小、不同个数、不同比例的 anchor，下面进行详细分析。

以 SSD300 为例，其提出了一个公式进行设计：

公式的含义是：输出特征图从大到小，其 anchor 尺寸设定遵循线性递增规则：随着特征图大小降低，先验框尺度线性增加，从而实现大特征图检测小物体，小特征图检测大物体效果。这里的 m 是值特征图个数，例如 ssd300 为 6，ssd512 为 7。第一层 conv4*3 是单独设置，不采用上述公式，$s_k$ 表示先验框大小相对于图片的 base 比例，而$s_{min}$、$s_{max}$ 表示比例的最小和最大值，voc 数据集默认是 0.2 和 0.9，coco 数据集默认是 0.15 和 0.9。

需要注意的是：作者提供的 caffe 版本代码和上面的公式比较难对应，而且 mmdet 里面实现也没有完全按照上面公式来写代码，故为了简单的描述该过程，本文采用 mmdet 代码流程来分析。虽然实现有一点点不一样，但是最终的 anchor 设置是完全相同的。以 voc 数据集和 ssd300 为例进行详细描述(coco 数据也是一样，仅仅是第一个输出层设置不一样而已)

(1) 先算出每个输出特征图上 anchor 的最大和最小尺度

第一个输出层单独设置，其 min_size=300x10/100=30，max_size=300x20/100=60。 从第二个输出层开始，首先将 $s_{min}=0.2$ , $s_{max}=0.9$ 乘上 100 并且取整，得到 min_ratio 和 max_ratio，然后计算出 step 步长为:

int(np.floor(max_ratio - min_ratio) / (num_levels=6 - 2))

最后利用 step 计算得到每个输出层的 min_size 和 max_size

# 计算第2个输出图和第self.num_levels个特征图anchor的min_size和max_size
for ratio in range(int(min_ratio), int(max_ratio) + 1, step):
    min_sizes.append(int(300 * ratio / 100))
    max_sizes.append(int(300 * (ratio + step) / 100))

# 第1个输出图单独算min_size和max_size
if self.input_size == 300:
    # conv4_3层的anchor单独设置，不采用公式
    if basesize_ratio_range[0] == 0.15:  # SSD300 COCO
        min_sizes.insert(0, int(300 * 7 / 100))
        max_sizes.insert(0, int(300 * 15 / 100))
    elif basesize_ratio_range[0] == 0.2:  # SSD300 VOC
        min_sizes.insert(0, int(300 * 10 / 100))
        max_sizes.insert(0, int(300 * 20 / 100))

这样就可以得到 6 个输出图所需要的 min_size 和 min_size 数值，注意这是原图尺度。

(2) 计算(0,0)特征图坐标处的 anchor 尺度和高宽比

首先配置参数为 ratios=[[2], [2, 3], [2, 3], [2, 3], [2], [2]])，如果某一层的比例是 2，那么表示实际高宽比例是 [1,1/2,2]，如果是 3，则表示 [1,1/3,3],可以看出如果某一层 ratio 设置为 [2,3]，那么实际上比例有 [1,2,3,1/2,1/3] 共 5 种比例，而尺度固定为 [1., np.sqrt(max_sizes[k] / min_sizes[k])]，k 为对应的输出层索引。

带目前为止，6 个特征图对应的 anchor 个数为[2x3=6,2x5=10,10,10,6,6],表示各种比例和尺度的乘积。

(3) 利用 base 值、anchor 尺度和高宽比计算得到每层特征图上(0,0)位置的实际 anchor 值

这个计算就和常规的 faster rcnn 完全相同了,计算(0,0)点处的实际宽高，然后利用中心偏移值得到所有 anchor 的 xyxy 坐标。

但是 SSD 里面不同输出层 anchor 个数不一样，故在得到所有 anchor 的 xyxy 坐标后，还需要进行筛选：

indices = list(range(len(self.ratios[i])))
indices.insert(1, len(indices))
base_anchors = torch.index_select(base_anchors, 0,
                                    torch.LongTensor(indices))

以 conv4_3 为例分析： conv4_3 预测层是需要 4 个 anchor，而上面其实生成了 6 个 anchor，base size 是 min_sizes[k])，也就是其在没有乘上 base size 前的 size 排列是

1,
1/2,
2,
1 * np.sqrt(max_sizes[0] / min_sizes[0]),
1/2 * np.sqrt(max_sizes[0] / min_sizes[0]),
2 * np.sqrt(max_sizes[0] / min_sizes[0])

而我们实际上仅仅需要以下 4 个：

1,
1/2,
2,
1 * np.sqrt(max_sizes[0] / min_sizes[0]),

对于 conv6 其需要 6 个 anchor，但是前面生成了 10 个，也就是说抛弃以下 anchor size 即可：

3,
1/3,
3 * np.sqrt(max_sizes[1] / min_sizes[1],
1/3 * np.sqrt(max_sizes[1] / min_sizes[1]),

对于其他输出层 anchor 的个数分析也是完全一样。最终 6 个特征图对应的 anchor 个数为 [4,6,6,6,4,4]

(4) 对特征图所有位置计算 anchor

直接将特征图上坐标点的每个位置都设置一份和(0,0)坐标除了中心坐标不同其余都相同的 anchor 即可，也就是将(0,0)特征图位置上面的 anchor 推广到所有位置坐标上。 基于前面的分析，SSD300 一共有 $8732 = 38\times 38\times 4+19\times 19\times 6+10\times 10\times 6+5\times 5\times 6+3 \times 3\times 4+1\times1\times4$ 个 anchor。 在得到整个 SSD 算法的所有 anchor 后，需要确定哪些 anchor 是正样本，其计算规则采用的是 faster rcnn 中采用的 MaxIoUAssigner，但是由于阈值设置不一样，故解释也不一样：

assigner=dict(
    type='MaxIoUAssigner',
    pos_iou_thr=0.5,
    neg_iou_thr=0.5,
    min_pos_iou=0.,
    ignore_iof_thr=-1,
    gt_max_assign_all=False)

其规则如下：

• 对每个 gt bbox 进行遍历，然后和所有 anchor(包括所有输出层)计算 iou，找出最大 iou 对应的 anchor，那么该 anchor 就负责该 gt bbox 即该 anchor 是正样本，该策略保证每个 gt bbox 一定有一个 anchor 进行匹配

• 对每个 anchor 进行遍历，然后和所有 gt bbox 计算 iou，找出最大 iou 值对应的 gt bbox，如果最大 iou 大于正样本阈值 0.5，那么该 anchor 也负责对应的 gt bbox，该 anchor 为正样本。该策略可以为每个 gt bbox 提供尽可能多的正样本

• 其余没有匹配上的 anchor 全部是负样本

论文中一个简单例子可以说明：

蓝色的猫会和(b)和(c)中的所有 anchor 进行匹配，基于 iou 准则，其仅仅会和(b)中的蓝色虚线框匹配上，而狗仅仅会和(c)的虚线红色框匹配上。

1.4 bbox 编解码

对于任何一个正样本 anchor 位置，其 gt bbox 编码方式采用的依然是 Faster rcnn 里面的变换规则 DeltaXYWHBBoxCoder 即

g 表示 gt bbox，d 表示 anchor，可以看出中心点 xy 预测是 gt bbox 中心点减掉 anchor 中心点，然后利用 anchor 的 wh 进行归一化，而 wh 预测是基于 gt bbox 的 wh 除以 anchor 的 wh，最后利用 log 来压缩大小 gt bbox 范围差异。

解码过程就只需要反向操作即可，比较简单。

1.5 loss 设计

对于分类分支来说，其采用的是 ce loss，而回归分支采用的是 smooth l1 loss，N 是所有 anchor 中正样本 anchor 的数量，回归分支仅仅计算正样本位置预测值 Loss。

前面说过经过匹配规则后存在大量负样本和少量正样本，对于分类分支来说这是一个极度不平衡的分类问题，如果不进行任何处理效果可能不太好，故作者采用了在线难负样本挖掘策略 ohem，具体是对负样本进行抽样，按照置信度误差或者说负样本分类 loss 进行降序排列，选取误差较大的 top-k 作为训练的负样本，以保证正负样本比例接近 1:3。

2 训练技巧

在 SSD 中提出应该采用大量有效的数据增强来提升目标检测性能。在 SSD 中其提出了：

1. 水平翻转

2. 随机裁剪、随机扩展和颜色扭曲

3. 基于预设 iou 范围进行随机裁剪块

需要特意说明的是(3)规则，其预设 min_ious=(0.1, 0.3, 0.5, 0.7, 0.9)，min_crop_size=0.3 范围。首先从 min_ious 列表里面随机选择某个 iou 取值，然后进行随机裁剪，只有当裁剪图片后的 gt bbox 和原图中的 gt bbox 的最小 iou 值不小于阈值才算成功，否则重新进行随机操作。以下是一个简单的例子：

左边是原图，右边是随机裁剪加上颜色扭曲的结果图。

3 测试流程

以 SSD300 为例：

1. 对输入图片进行前处理，变成指定大小输入到网络中，输出 8732 个基于 anchor 的预测值，其中任何一个都包括分类长度为 num_class+1 的向量，和回归长度为 4 的向量

2. 首先对分类分支取出预测类别和对应的预测分值，过滤掉低于 score_thr 阈值的预测值

3. 对剩下的 anchor 利用回归分支预测值进行 bbox 解码，得到实际预测 bbox 值

4. 对所有 bbox 按照类别进行 nms 操作，得到最终预测 bbox 和类别信息

4 结果分析

4.1 多尺度预测重要性

可以看出多尺度预测情况下可以提升性能。

4.2 anchor 重要性

为了说明为啥要设置这么密集的 anchor，作者做了大量实验，首先感受下 SSD 相比其余算法的 anchor 数目差异：

可以发现 SSD 远远多于其余算法。实验结果如下所示：

当包括更多 anchor 比例后，对应性能也有提升，并且 SSD 采用了 OHEM 策略可以在一定程度缓解由于 anchor 设置过密带来的正负样本不平衡问题。

4.3 数据增强重要性

通过上表可以发现，高效的数据增强操作可以大幅提高目标检测性能。

4.4 总体性能

精度对比：

速度对比：

整体综合效果图如下：

5 总结

SSD 基于 Faster rcnn 的思想，将其应用于 One-stage 目标检测中，实现了速度和精度的平衡。最大贡献是验证了多尺度预测、密集 anchor 设置附加 ohem 策略以及高效数据增强对整体算法的性能提升，其采用的核心操作依然是目前目标检测的主流做法。

参考文献

1. SSD: Single Shot MultiBox Detector

2. https://link.zhihu.com/?target=http%3A//www.cs.unc.edu/~wliu/papers/ssd_eccv2016_slide.pdf

3. https://jonathan-hui.medium.com/ssd-object-detection-single-shot-multibox-detector-for-real-time-processing-9bd8deac0e06